Десетте най-важни числа в историята на науката


Приложение: Пи е ключова константа в много уравнения, които се прилагат в сферата на хармоничния анализ. Освен в математиката, то има широка употреба и в други точни науки като механиката и физиката.
На второ място е:
Ойлеровото число, наричано още неперово число. То също е една от най-важните математически константи. Ойлеровото число е основа на естествените логаритми и има широко приложение в математиката със своята „скромна“ стойност 2,718281828459 (съкратена версия).
Може да бъде представено по два начина:
– като граница на числова редица,
– като сума на безкраен ред.
Числото е се нарича Неперово в чест на шотландския учен Джон Непер – автор на съчинението „Описание на удивителните таблици на логаритмите“ (1614 г.).
За първи път константата негласно присъства в приложение към превода на английски език на споменатата работа на Непер. Предполага се, че автор на приложението е английският математик Уилям Оутред. Самата константа е изведена за първи път от Якоб Бернули . Буквата е първи използва Ойлер през 1727 г., а първата публикация с тази буква е неговата „Механика или Наука за движението, изложена аналитично“. Поради това е понякога е наричано „число на Ойлер“.
/ Леонард Ойлер / Приложение: В сферата на финансите, неперовото число се използва за определяне на сложната лихва, помагайки ни да дефинираме времевата стойност на парите. Освен това, Ойлеровото число играе своята роля и при описанието на процеси на разлагане на химични съединения – например радиовъглеродното датиране.
Приложение: В сферата на финансите, неперовото число се използва за определяне на сложната лихва, помагайки ни да дефинираме времевата стойност на парите. Освен това, Ойлеровото число играе своята роля и при описанието на процеси на разлагане на химични съединения – например радиовъглеродното датиране.
На трето място е:
златното сечение, още познато като златна пропорция или божествена пропорция. Това е число, което често срещаме в геометрията, най-вече при фигури, свързани с петоъгълна симетрия. φ закръглено е =1,6180.
 Приложение: Златното сечение е едно наистина всестранно развито число. То се ползва и във финансовите анализи, когато се правят опити да се определи дали даден пазар ще продължи своя темп на развитие или ще се отклони. Изключително важно е златното сечение и за архитектурата и изкуството, като това му название е дадено не от кого да е друг, а от самия Леонардо да Винчи. За него то е било пропорцията за „идеалното човешко тяло“. Повече за него вижте тук.
Приложение: Златното сечение е едно наистина всестранно развито число. То се ползва и във финансовите анализи, когато се правят опити да се определи дали даден пазар ще продължи своя темп на развитие или ще се отклони. Изключително важно е златното сечение и за архитектурата и изкуството, като това му название е дадено не от кого да е друг, а от самия Леонардо да Винчи. За него то е било пропорцията за „идеалното човешко тяло“. Повече за него вижте тук.
На четвърто място е:
константата на Планк. Тя е основна константа в квантовата механика, свързваща енергията на електромагнитна вълна с нейната честота. 
Наречена е така в чест на Макс Планк, един от основоположниците на квантовата механика.
Има следната стойност:
-
 Константата на Планк свързва честотата
Константата на Планк свързва честотата  и енергията на фотон:
и енергията на фотон:
Е=h. v, както и свързва импулса p на частица с дължината на вълната  на нейната материална вълна (вълна на де Бройл):
на нейната материална вълна (вълна на де Бройл):
Вернер Хайзенберг, легендарен немски физик, използва константата на Планк, за да дефинира по-добре своя знаменит „Принцип на неопределеността“.
Приложение: Някои автори смятат, че Принципът на неопределеността може да бъде използван, за да определи стабилността и устойчивостта на даден финансов инструмент. Квантовият компютър все още е на ниво теоретичност, но ако се появи и като реален уред в скоро време, може да си говорим за неповторим принос на Принципа, а покрай него – и на константата на Планк към прогреса на човечеството.
На пето място е:
числото на Авогадро, или константата на Авогадро, което има стойност 6.0221515 x 1023. То се използва за определянето на броя на градивните частици /атоми, молекули или йони/ в определено количество вещество.
Приложение: Числото на Авогадро е интересна взаимовръзка между огромно количество от различни химични свойства. Химичните инженери имат огромна полза от константата в сферата на стехиометрията (изчислителните задачи по химия). То е основа и за определянето на единицата мол: един мол въглерод съдържа точно 6,022 х 1023 въглеродни атома и тежи 12,011 грама, атомната маса на въглерода.
На шесто място е:
константата с, определяща скоростта на светлината. Тя е 299,792,458 метра в секунда. Скоростта на светлината е една изключително важна физична константа и променя облика на физиката, както и подбужда много интересни въпроси. В теорията на относителността c свързва времето и пространството. Експерименталното определяне на точната стойност на c започва още през 1676 г., когато датският астроном Оле Рьомер доказва, че скоростта на светлината не е безкрайна, като наблюдава движението на Йо – луната на Юпитер. През 1905 г. Алберт Айнщайн постулира, че скоростта на светлината във вакуум е независима от движението или от отправната система и изследвайки последиците от този постулат, извежда своята Специална теория на относителността. Същевременно Айнщайн демонстрира, че c има голямо значение и извън контекста на светлината и електромагнетизма. Затова нараства значението на определянето на точната ѝ стойност. След векове на все по-точни измервания през 1975 г. скоростта на светлината е измерена на 299 792 458 m.s-1 През 1983 г. се прави предефиниране на метъра в Международна система единици (SI) като той се определя като разстоянието, изминато от светлината във вакуум за 1/299 792 458 (една 299 792 458-ма) част от стандартната секунда. В резултат на това числената стойност на c сега е обвързана точно с дефиницията на метъра.
Приложение: Константата се използва в много различни по-висши математически формули и най-вече при сферата на анализирането на пътуването в Космоса. Освен всичко друго, тя се крие и като буквата „c” в знаменитата Теория на относителността на Алберт Айнщайн E = mc2.
Интересни факти:
- Светлината на Слънцето достига до Земята за 8 минути, а автомобил би изминал това разстояние за 180 години, ако се движи със скорост 60 km/h.
- Светлината изминава един метър за 3,3 наносекунди
- Светлината изминава един километър за 3,3 микросекунди
- Светлината изминава разстоянието от геостационарната орбита до Земята за 0,12 секунди
- Светлината обикаля Земята по екватора за 0,13 секунди
- Светлината изминава разстоянието от Земята до Луната за 1,3 секунди
- Светлината изминава разстоянието от един парсек за 3,26 години
- Светлината изминава разстоянието от Алфа Кентавър до Земята за 4,4 години
- Светлината прекосява Млечния път за 100 000 години
- Светлината изминава разстоянието от галактиката Андромеда до Земята за 2 500 000 години.
На седмо място е:
гравитационната константа G. Тя се изчислява на 6.67300 x 10-11 m3 kg-1 s-2.
/ торзионна везна /
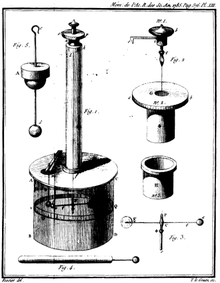 Гравитационната константа е измерена за пръв от Хенри Кавендиш през през 1798 г., а най-точната стойност на G е получена чрез измерване на взаимното привличане на две известни маси с торзионна везна.
Гравитационната константа е измерена за пръв от Хенри Кавендиш през през 1798 г., а най-точната стойност на G е получена чрез измерване на взаимното привличане на две известни маси с торзионна везна. 
/ Х. Кавендиш /
Приложение:
G определя силата на привличане между две тела. Изключително важна е при механоинженерството, аероинженерството и гражданското инженерство. Като прост пример при изграждането на мостове може да се посочи фактът, че инженерът трябва да се увери, че мостът ще може да функционира както имайки предвид тежестта на колите, така и принципното присъствие на гравитационната константа.
На осмо място е:
константата на Болцман, обозначаваща се с k. Тя е фундаментална физична константа, която участва в почти всяка формула в сферата на физиката и квантовата физика. Самият Болцман за пръв път я използва в своята формула за ентропията от 1873 година. Равна е на газовата константа R разделена на числото на Авогадро Na, k = R/Na. Стойността и е:
![]() JK-1
JK-1
Приложение: Константата на Болцман ни помага да разберем защо ледът се топи в топла вода, но същевременно не се формира в хладка вода. Тя е повратна за традиционната и квантовата физика.
имагинерната единица. Тя е равна на корен квадратен от -1, което значи, че имагинерната единица на втора степен е равна на -1. Имагинерната единица i позволява системата на реалните числа да се разшири до системата на комплексните числа.
Комплексните числа са се появили най-напред като „мними (въображаеми) величини“ в труда на Кардано (1545 г.) „Великото изкуство, или за алгебричните правила“. Той считал, че са негодни за употреба. Ползата от мнимите величини първи е оценил Бомбели (1572 г.) – при решаването на кубични уравнения, когато реалните корени се изразяват чрез кубични корени от мними величини. Той дава най-простите правила за действия с комплексни числа.
През XVI – XVII в. математиците започват да наричат „мними“ изрази, появяващи се при решаване на квадратни и кубични уравнения.
Задачата за изразяване на n-ти корен от дадено число е решена в работите на Моавър и Р. Котес (1722 г.). Символът i= квадратен корен от -1 е предложен от Ойлер (1794 г.), който използва първата буква от „imaginarius“. През 1751 г. той изказва мисълта за алгебрична затвореност на полето на комплексните числа. До същия извод стига и д’Аламбер (1747 г.), но първото строго доказателство на този факт е дадено от Гаус (1799 г.). Той въвежда в употреба термина „комплексно число“ през 1831 г.
По определение, имагинерната единица i е едното решение(от две възможни) на квадратното уравнение 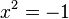 .
.
Степените на i се повтарят циклично. За да видите съответните степени на имагинерната единица, щракнете тук.
Приложение: Полиномите на реалната променлива x често се прилагат в ежедневието, а самата имагинерна единица има приложение както в математиката, така и във физиката и в инженерните науки.
Ойлеровото уравнение, което свързва доста неща в едно. Формулата на Ойлер гласи, че за всяко реално число φ :
неперовото число е повдигнато на степен i.φ е равно на сбора от изразите cos φ и i. sin φ.
- където: е — основа на натуралния логаритъм,
- i — имагинерна единица, sin и cos са тригонометрични функции.
Ричард Файнман нарича формулата на Ойлер „скъпоценен камък“ и „най-важната формула“ в цялата математика. Ако искаме да обясним тази формула с най-прости думи, това е равносилно на ротация на единичен вектор на ъгъл φ.
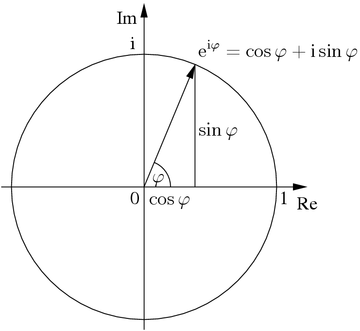 Формулата се оказва изключително елегантна поради факта, че съчетава най-известните математически константи, както и 0, 1 и “i”.
Формулата се оказва изключително елегантна поради факта, че съчетава най-известните математически константи, както и 0, 1 и “i”.
Приложение: Това, което уравнението описва, е “разхождането“ по цяла окръжност в комплексна (z) равнина. Докато реалната стойност не достигне -1.

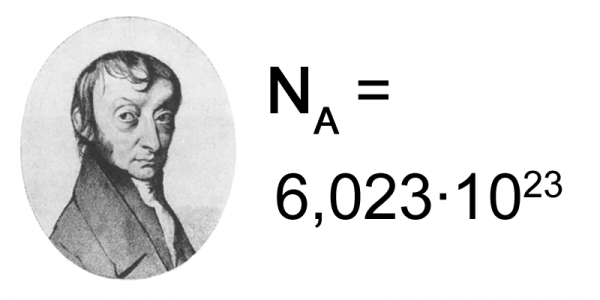

Как е възможно да е имало толкова умни хора през тези мрачни векове? Когато почти 100% са били неграмотни. А и сега не можем да ги разберем.
Има ли нехомогенност в числата на Фибоначи, след като може би съществува привилегировано число, което се отличава по свойства от всички други в реда (а наистина ли е така?) – единствено числото 5 има свойството да се намира на пореден номер в редицата, който съвпада със самото число, ако не се брои нулата? Ха!
Стефан
На 12-то място в редицата е 144 = 12 * 12. Ако се задълбочи човек, убедена съм ще намери и други съвпадения.
Защо не може да се намери точната константа на „Пи“? Защото никой не може да измери абсолютните дължини на окръжността и диаметърът й,а от там да се получи точното съотношение.
Защо не може да се намери точната константа на „Пи“? Защото никой не може да измери абсолютните дължини на окръжността и диаметърът й,а от там да се получи точното съотношение.
Защо не може да се намери точната константа на „Пи“? Защото никой не може да измери абсолютните дължини на окръжността и диаметърът й,а от там да се получи точното съотношение.
Това под номер 10 не е константа, а формулата на Ойлер.